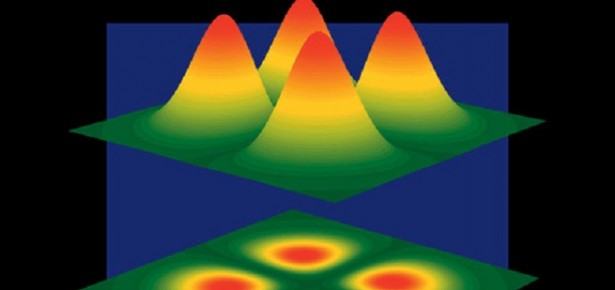
Phenomena of spontaneous pattern formation, both of spatial and of temporal nature, are ubiquitous in the vast domain of nonlinear dynamical systems, encompassing for example hydrodynamics, chemistry, biology, population dynamics, and social sciences. The LLE was conceived by following a criterion of simplicity, which led to the selection of an optical ring cavity containing a medium with a cubic Kerr nonlinearity and driven by a stationary coherent input field. The combination of the Kerr nonlinearity and of light diffraction gives rise to a rich variety of 1D and 2D patterns, and to cavity solitons, which develop in the transverse planes orthogonal to the longitudinal direction of propagation of light in the cavity.
Some years after the introduction of the LLE Haelterman, Trillo and Wabnitz formulated the temporal/longitudinal version of the equation, in which diffraction is replaced by group velocity dispersion. In this case patterns and cavity solitons develop in the longitudinal direction, propagate along the cavity with the light velocity and generate a periodic train of pulses in the output of the cavity itself.. In this way, the LLE unifies spatial phenomena that arise in the transverse planes, with spatio-temporal effects that occur in the longitudinal direction.
Optical frequency combs are sets of equidistant frequency lines in short-pulse mode-locked lasers. Their discovery by John Hall and Theodor Haensch (who received the 2005 Nobel Prize in Physics for this achievement) revolutionized the measurement of frequencies and opened out a vast scenario of applications. In 2007 Kippenberg and his group demonstrated the realization of broadband frequency combs using the whispering gallery modes in high-Q microresonators containing Kerr media .The generation of such combs occurs from the four-wave mixing processes activated by the interaction of the monochromatic driving field, injected with a frequency resonant with a cavity mode, and the Kerr medium. Thus such systems con be considered as novel multi-wavelength coherent sources, where all the lines, except the central one corresponding to the driving frequency, are created by the gain induced by the four-wave mixing. Kerr frequency combs, generated in microresonators such as that shown in Fig. 1,

Fig.1. Christallyne disk-resonator standing on top of a metallic stub. Courtesy Aurelien Coillet, FEMTO-ST, University of Besancon.
are foreseen to have a strong impact as a compact, low-cost, low-power, chip-compatible technology, and produce important applications to such fields as optical coherent communication in ultradense optical fiber networks, ultrastable microwave generation, spectroscopy, generation of entangled twin photon pairs with chip-scale resonators. This has stimulated a considerable worldwide effort in this approach [2].
It has become clear that the LLE is the model for the description of Kerr comb generation and the prediction of the comb characteristics as a function of the system parameters [2]. The spontaneous formation of travelling patterns along the cavity is the crucial mechanism which creates the combs and governs their features (see Fig. 2).
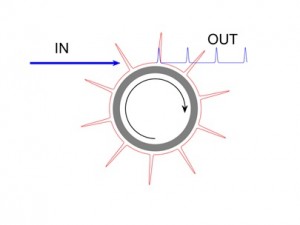
Fig.2. The injection of a uniform driving field on the left spontaneously generates, in the microring resonator, a pattern which travels clockwise and produces a periodic sequence of pulses in the output. In the frequency domain, the sequence of pulses corresponds to a broad band frequency comb.
The spectacular progress in the field of photonics, occurred from thirty years ago, has realized all the rather idealized conditions assumed by the LLE. A curious consequence of such a history is that this equation is even more used now than at the times immediately after its formulation.
In conclusion, the LLE represents a case of pattern formation which is immediately linked to a promising applicative avenue.
[1] L.A.Lugiato and R.Lefever, Spatial dissipative structures in passive optical systems, Phys. Rev. Lett. 58, 2209 (1987)
[2] Y.K.Chembo, Kerr optical frequency combs: theory, applications and perspectives, Nanophotonics 5, 214 (2016)
Latest Comments
Have your say!