Fifteen Eighty Four

You can read the entire excerpt from Games and Mathematics here.

Introduction

Abstract games, traditional puzzles and mathematics are closely related. They are often extremely old, they are easily appreciated across different cultures, unlike language and literature, and they are hardly affected by either history or geography. Thus the ancient Egyptian game of Mehen which was played on a spiral board and called after the serpent god of that name, disappeared from Egypt round about 2900–2800 BCE according to the archaeological record but reappeared in the Sudan in the 1920s. Another game which is illustrated in Egyptian tomb paintings is today called in Italian, morra, ‘the flashing of the fingers’ which has persisted over three thousand years without change or development. Each player shows a number of fingers while shouting his guess for the total fingers shown. It needs no equipment and it can be played anywhere but it does require, like many games, a modest ability to count [Tylor 1879/1971: 65].

As, of course, do dice games. Dice have been unearthed at the city of Shahr-i Sokhta, an archaeological site on the banks of the Helmand river in southeastern Iran dating back to 3000 BCE and they were popular among the Greeks and Romans as well as appearing in the Bible.

The earliest puzzles or board games and those found in ‘primitive’ societies tend to be fewer and simpler than more recent creations yet we can understand and appreciate them despite the vast differences in every other aspect of culture.

‘Culture’ is undoubtedly the right word: puzzles and games are not trivia, mere pleasant pastimes which offer fun and amusement but serious features of all human societies without exception – and they lead eventually to mathe- matics. String figures are a perfect example. They have been found in northern America among the Inuit, among the Navajo and Kwakiutl Indians, in Africa and Japan and among the Pacific islands and the Maori and Australian aborig- ines [Averkieva & Sherman 1992]. This is not necessarily evidence of ancient exchanges between cultures. It could just be that people everywhere tend to fiddle with bits of string – and the results can be very pleasing, like the Jacob’s ladder in Figure 1.

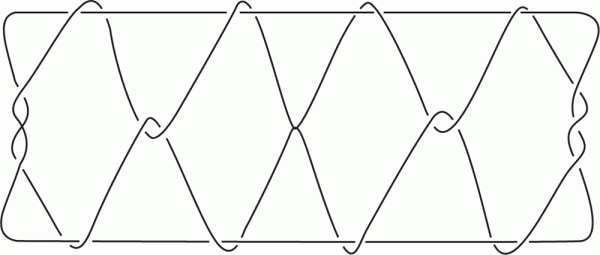Figure 1 Jacob’s Ladder

String figures are extremely abstract. Although usually made on two hands, or sometimes the hands and feet or with four hands, Jacob’s ladder would be recognisably ‘the same’ if it were fifty feet wide and made from a ship’s hawser, yet these abstract playful objects can also be useful. The earliest record of a string figure is the plinthios (Figure 2), described in a fourth-century Greek miscellany. It was recommended for supporting a fractured chin, and much resembles the Jacob’s ladder figure [Probert 1999].

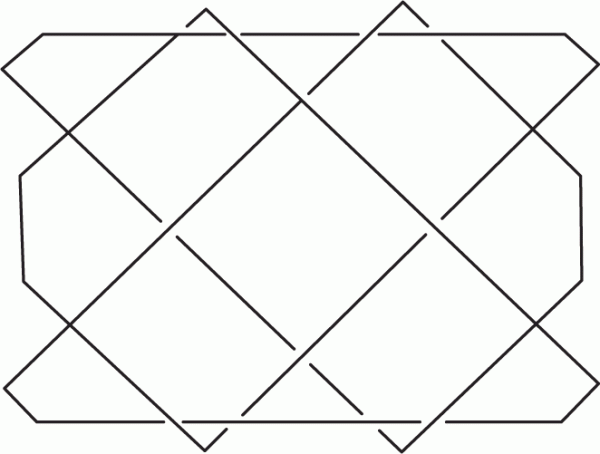Figure 2 Plinthios string figure

No surprise then that string figures are more than an anthropological curios- ity, that they are mathematically puzzling, related to everyday knots – including braiding, knitting, crochet and lace-work – and to one of the most recent branches of mathematics, topology.

The oldest written puzzle plausibly goes back to Ancient Egypt:

“There are seven houses each containing seven cats. Each cat kills seven mice and each mouse would have eaten seven ears of spelt. Each ear of spelt would have produced seven hekats of grain. What is the total of all these?”

This curiosity, paraphrased here, is problem 79 in the Rhind papyrus which was written about 1650 BC. Nearly 3000 years later in his Liber Abaci (1202), Fibonacci posed this problem:

“Seven old women are travelling to Rome, and each has seven mules. On each mule there are seven sacks, in each sack there are seven loaves of bread, in each loaf there are seven knives, and each knife has seven sheaths. The question is to find the total of all of them.”

It is tempting to suppose that these puzzles are related. If they are, could there be a historical connection across 5000 years with this riddle from the British eighteenth century Mother Goose collection?

“As I was going to St. Ives,
I met a man with seven wives.
Each wife had seven sacks,
Each sack had seven cats,
Each cat had seven kits;
Kits, cats, sacks and wives,
How many were going to St. Ives?”

Another widespread puzzle concerns a man, a wolf, a goat and a cabbage, to be transported across a river in a small boat, never leaving the wolf alone with the goat or the goat alone with the cabbage. It first appeared in a collection attributed to the medieval scholar Alcuin of York (735–804), Propositions to Sharpen the Young [Alcuin of York 1992].

Tartaglia (1500–1557) who famously solved the cubic equation and then gave the solution to Cardan who scandalously broke his solemn agreement not to publish it, printed a version featuring three brides and their jealous husbands who have to cross a river in a boat that will only take two people. If no bride can be accompanied by another women’s future husband, how many trips are required?

Essentially the same puzzle is also found in Africa, in Ethiopia, in the Cape Verde Islands, in Cameroon, and among the Kpelle of Liberia and elsewhere. Since these African versions are often logically distinct from the Western, they may well be entirely independent: the difficulty of transporting uncongenial items across a river used to be universal [Ascher 1990].

Read the entire excerpt from Games and Mathematics here.