After last week’s imaginative speculation, I’d better tell you something concrete. How about the solution to quantum gravity that has been eluding us for some 90 years? Here it is … er … with one minor catch. We’ll have to suppose that spacetime is 3 dimensional, i.e. one time and only two space directions rather than three.

He’s never heard of this “3rd spatial dimension”!
There is a tradition, starting I think with Edwin A. Abbott’s 1880 tale ‘Flatland’, where we suppose that we are not 3-dimensional beings but, let us say, ants, constrained to live forever on some two-dimensional surface. We tend to visualize a surface — imagine, say, the surface of a sphere or doughnut — within three dimensions, but don’t be fooled by that. That is just an aid to visualization. An ant crawling about on the surface, moving along ‘shortest paths’ (the analogue of a straight line on a flat space) could fully map out the geometry of the surface without ever leaving it.
I am speaking here of the spatial geometry. We will assume that time is a further linear dimension, making spacetime 3-dimensional, mapped out as the 2-dimensional surface evolves in time.
Actually, we won’t assume any of this, since as I explained in previous blogs, there is no evidence of an actual spacetime continuum of any dimension. But we will take it as a commonly accepted starting point and then I will explain carefully where we have to make the quantum leap to throw all that away to get to actual quantum gravity. This will also give you a bit of insight into the guts of the way that scientific revolutions work in practice.
Now, you may ask, in this day and age, where string theorists are happy to work in 10500 dimensions: what is so special about three? In any dimension the modern way of thinking about gravity is in terms of a ‘metric’. This is a gadget which at each point of spacetime allows one to compute the distance to all nearby points. It goes back to the 19th century mathematician Riemann and was used by Einstein. The mathematicians Cartan and Weyl found a different way of thinking about this in terms of a ‘frame’ and a ‘connection’ at any point of the spacetime. Their theory works in any dimension but I am going to cut straight to a very special answer only in three spacetime dimensions.
First, think about what you can do to a rigid object in three flat dimensions (in our case one of these is time but you will be able to visualise better if you dont worry about that). Well, you can move the object around and you can rotate it. Together these form a classical symmetry group E_3 of ‘translations and rotations’ in three dimensions. The same in a three dimensional flat spacetime.
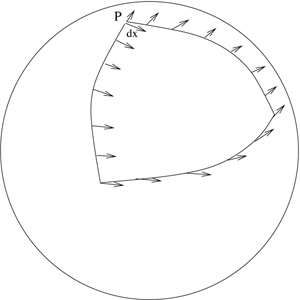 What the Cartan-Weyl theory amounts to in three dimensions is to express the metric geometry of spacetime in terms of a gadget that assigns to every loop in spacetime an element of E_3. This is the translation and rotation matrix for transport around the loop. Let me just show you an example to get the idea. Referring to the figure, suppose you start at point P and keep your eye on an infinitesimal displacement dx (a differential in the language of two posts ago). Now suppose you move along the loop keeping the angle to the direction of motion fixed. Try it out on a globe at home; the arcs are supposed to be quarter great circles and P is the north pole. When you get back to P will you still be pointing the same way as the original dx? Not necessarily when the geometry is curved! Instead there will be some rotation’ that relates the result to the orignal dx, about 90 degrees in the example. This is how connections are handled in the Cartan-Weyl theory; the new twist is that frames can be viewed as enlarging a usual connection so that they assign not just rotations but ‘translations and rotations’ to each loop. This enlarged connection gadget encodes all of the geometry of our three-dimensional spacetime, including its curvature.
What the Cartan-Weyl theory amounts to in three dimensions is to express the metric geometry of spacetime in terms of a gadget that assigns to every loop in spacetime an element of E_3. This is the translation and rotation matrix for transport around the loop. Let me just show you an example to get the idea. Referring to the figure, suppose you start at point P and keep your eye on an infinitesimal displacement dx (a differential in the language of two posts ago). Now suppose you move along the loop keeping the angle to the direction of motion fixed. Try it out on a globe at home; the arcs are supposed to be quarter great circles and P is the north pole. When you get back to P will you still be pointing the same way as the original dx? Not necessarily when the geometry is curved! Instead there will be some rotation’ that relates the result to the orignal dx, about 90 degrees in the example. This is how connections are handled in the Cartan-Weyl theory; the new twist is that frames can be viewed as enlarging a usual connection so that they assign not just rotations but ‘translations and rotations’ to each loop. This enlarged connection gadget encodes all of the geometry of our three-dimensional spacetime, including its curvature.
Now, in this new language, Einstein’s equations in a vacuum, that control how spacetime curves, is expressed simply as follows: the element of E_3 given by transporting round a loop does not change as you move the loop a little. And when there is matter, which for our purposes we idealise as perfect points in space (or lines in spacetime), the same is true as long as your curve does not cross one of these particles. From this, you can see that the connection gadget is fully specified by choosing a certain fixed number of elements of E_3; you have E_3 elements associated to loops that go around any of the point particles, and you have E_3 elements associated to loops that wrap around the surface that we are crawling around on. Even though the geometry of the surface may evolve in time its number of holes, i.e. its topology is assumed not to change. Under these technical assumptions the entire geometry and Einstein’s equations for gravity is now encoded in some fixed number of elements of the symmetry group E_3.
So much for classical gravity in three dimensions. Now we are ready for quantum gravity. In conventional physics there is an elaborate ‘machinery’ of quantisation. In fact there are two, the Feynman path integral and the Heisenberg algebra method (known in physics as canonical quantisation). Both of them are fundamentally flawed but for rather different reasons.
The Feynman path integral is based on the idea that classical mechanical systems are governed by a quantity called the ‘action’ (basically, it is like the energy) which is ‘minimized’ when the classical equations of motion are obeys. The quantum theory is defined by summing over all possible classical configurations with a weighting given by the classical action. This kind of works to first approximation more or less ‘by design’. It is very much like a statistician cooking up some random variables out of the average values that they want the random variables to obey. It is putting the cart before the horse: the classical continuum geometry should emerge out of some deeper principle for the quantum theory. I covered this point in my post on religion and science.
The Heisenberg algebra method consists of the idea that in classical mechanics one can carefully chose variables’ ‘coordinates’ in a special form similar to position and momentum in quantum mechanics. One then quantises the theory by replacing these classical variables by quantum ones obeying the famous Heisenberg relations. Personally, I think this is a bit more on the right track but I would have to say — why limit ourselves to the Heisenberg algebra? The honest answer is that until about 20 years ago this algebra (and perhaps the angular momentum algebra) was the only algebra familiar to physicists. In other words, mainly a lack of imagination.
This was exploded in the late 1980s with the arrival of quantum symmetry and quantum or noncommutative geometry. From the point of view of a quantum geometer like me, limiting ourselves to the Heisenberg algebra is analogous to assuming that the Earth is flat, whereas the actual possibilities mathematically are much richer.
In our case, there is a mathematically clear choice of quantum symmetry ‘quantum E_3’. So, how do we quantise quantum gravity in three spacetime dimensions? Just replace E_3 by the quantum version of E_3. Most classical symmetries have well-established quantum versions and this is one of them. Hey, Presto! We are done and we have just quantized gravity in three dimensions with point-particles as matter. Notice the critical point where we actually throw away all of the ‘continuum baggage’ and replace it by a deeper (quantum symmetry) principle. But we retain the ability to recover it in a special approximation where the quantum symmetry behaves almost classically, which is as it should be.
There is more. We know from astronomy that there seems to be some mysterious dark energy or ‘cosmological constant’ needed in our actual (albeit four dimensional) Universe. In the three dimensional model this arises very naturally as follows. At the level of classical gravity we must replace E_3 by a group SL_2 of 2 x 2 matrices of determinant 1. (The determinant of a 2 x 2 matrix is the product of the diagonal minus the product of the off- diagonal entries.) The difference between this and E_3 is that ‘translations’ are replaced by something a bit more complicated. But this too has a quantum symmetry version. Now, I mentioned in my post on quantum symmetry that the very concept involved a ‘arrow reversal’ duality in which one could reverse things, replacing the quantum symmetry by a ‘dual’ quantum symmetry. When you do this to the translation-like part of the quantum version of SL_2 you, more or less, get an equivalent theory.
In short, quantum gravity in three dimensions with cosmological constant or dark energy is self dual under a certain duality operation. This is lost if one worked with plain quantum gravity without the dark energy, i.e  could explain why it is there. And this self-duality is, as I explain in my chapter of the multiauthored volume On Space and Time, a deep principle for quantum gravity. We had a first taste of it, at a speculative level, last week.
could explain why it is there. And this self-duality is, as I explain in my chapter of the multiauthored volume On Space and Time, a deep principle for quantum gravity. We had a first taste of it, at a speculative level, last week.
Editor’s Note: Shahn Majid has been talking around his research with B Schroers in “q-Deformation and semidualisation in 3D quantum gravity” arXiv:0806.2587.
Latest Comments
Have your say!